Ex-01
O esquema representa um
triângulo inscrito num círculo de raio R. Na figura estão indicadas as medidas
de dois arcos e um dos lados do triângulo. Determine:
a) O valor do raio R;
b) A medida do lado AC;
c) Medida do lado maior do
triângulo ABC.
Solução:
a) No triângulo ∆BOC:
Por
Teorema de Pitágoras:
b) No triângulo ∆AOC:
Por lei dos cossenos:
O
ângulo AÔC = 120º (tem o mesmo valor que o arco AC)
c) No triângulo ∆AOB:
Por lei dos senos:
O ângulo AÔB = 150º (tem o
mesmo valor que o arco AB)
O
arco AB = 150º, pois 360º = AB+90+120 → AB=150º
Por lei dos cossenos:

Podemos notar que os resultados parecem
diferentes, mas, são iguais. Prova-se
com pequenas manipulações algébricas:
Demonstração:
Seja x o valor obtido pela
lei dos senos:
E seja y o valor obtido pela
lei dos cossenos:
Vamos demonstrar que x = y, partindo de y:
EX-02
Um triângulo tem dois lados
medindo 3 m
e 5 m . O
ângulo formado por eles mede 120º. Assim sendo, calcular:
a) A medida do terceiro lado
é:
b) O diâmetro do círculo
circunscrito ao triângulo mede:
Solução:
a) Seja x a medida do
terceiro lado, então, por lei dos cossenos tem-se:
b) Seja R o raio do círculo
que circunscreve o triângulo, então, tem-se:
O ângulo BÂC = 120º (pelo
enunciado) → O arco BC = 120º → O ângulo BÔC = 120º.
Portanto, aplicando lei dos
senos no triângulo ∆BOC,
EX-03
Os lados de um triângulo
medem 5 m ,
6 m e 7 m . Se x é o menor ângulo do
triângulo, determinar o valor do cosseno de x?
Solução
Por aplicação da lei dos
cossenos:
EX-04
Determinar o raio do círculo
circunscrito ao triângulo, da questão anterior.
Solução
Pela relação entre ângulo
central e ângulo inscrito, tem-se: y =
2x
Veja mais sobre ângulo central e inscrito: clique aqui
Aplicando a lei dos cossenos
em triângulo ∆AOB, tem-se,
EX-05
No triângulo de desenho,
determinar o lado x em função do lado (5) e dos ângulos dados (α e 2α).
Solução:
Aplicando a lei dos senos:
EX-06
Num retângulo, veja a
figura, os lados medem 3 m
e 6 m .
Seja x é a medida do ângulo agudo, formado pelas diagonais. Determine sen(x), x e sen(y).
Solução:
Pelo Teorema de Pitágoras
(∆ABC), tem-se:
Cálculo do sen(x)
e x:
Pela lei dos cossenos (∆COD),
tem-se:
Sabemos que sen²(x) +
cos²(x) = 1
Cálculo do
sen(y):
Pegando o triângulo ∆ABD:
EX-07 (FUVEST-SP)
Em um triângulo ABC o lado
AB mede 4√2 e o ângulo C, oposto ao lado AB, mede 45º. Determine o raio da
circunferência que circunscreve o triângulo.
Solução
Representando
geometricamente o enunciado tem-se que:
Pela lei dos senos:
EX-08
A figura mostra o trecho de
um rio onde se deseja construir uma ponte AB. De um ponto P, a 100 m de B, mediu-se o ângulo
APB = 45º e do ponto A, mediu-se o ângulo PAB = 30º. Calcular o comprimento da
ponte.
Solução:
Colocando os dados do
enunciado no desenho, tem-se:
Pela lei dos senos (∆APB):
EX-09 (FEI)
Calcule c, sabendo que a =
4, b = 3√2 e C = 45º.
Solução:
Aplicando a lei dos cossenos,
tem-se:
EX-10 (FEI)
Num triângulo ABC, BC=a,
AC=b, Â=45º e B=30º. Qual é o valor de a, sendo a+b=1+√2?
Solução:
Aplicando a sei dos senos:






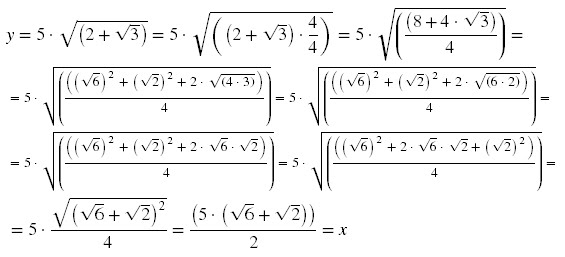













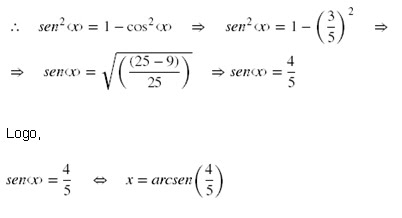












Nenhum comentário:
Postar um comentário