EX-01
Calcular sen(7π/12).
Solução:
Aplicando a adição de
arcos
Resposta:
EX-02
Sendo a – b = π/3, determinar o valor de:
y = (cos a + cos b)² + (sen a + sen b)² .
Solução:
(cos a)² = (cos(a))² = cos²(a) = cos² a
y=cos²(a)+2cos(a)cos(b)+cos²(b)+sen²(a)+
+2sen(a)sen(b)+sen²(b)
y=cos²(a)+sen²(a)+cos²(b)+sen²(b)+2cos(a)cos(b) +2sen(a)sen(b)
y= 1 + 1 + 2cos(a)cos(b)+2sen(a)sen(b)
y= 2 + 2cos(a)cos(b)+2sen(a)sen(b) =
y= 2+2[cos(a)cos(b)+sen(a)sen(b)]
=
= 2+2[cos(a-b)]=2+2cos(π/3)
y = 2 + 2*1/2 = 3
Resposta: y = 3
EX-03
Provar a identidade:
sen(x + y).sen(x - y) = sen²x – sen²y = cos²y – cos²x
Solução:
sen(x + y).sen(x - y) =
= (senx.cosy
+ seny.cosx).(senx.cosy
– seny.cosx) =
= (senx.cosy)² - (seny.cosx)² = sen²x.cos²y –
sen²y.cos²x = (I)
[sen²β + cos²β =1 → cos²β = 1 –
sen²β]
(I) = sen²x.(1 - sen²y) – sen²y.(1 – sen²x) =
= sen²x - sen²x.sen²y – sen²y + sen²y.sen²x = sen²x – sen²y
[sen²β +
cos²β =1 → sen²β = 1 -
cos²β]
(I) = (1 – cos²x).cos²y – (1 – cos²y).cos²x =
= cos²y – cos²x.cos²y – cos²x + cos²y.cos²x = cos²y – cos²x
EX-04
Determinar o
valor de sen(α – β),
sabendo-se que senα = 7/25,
(0 < α < π/2) e cosβ =
4/5, (3π/2 < β <
2π).
Solução:
Sabemos que:
sen²x + cos²y = 1
Então,
senα
= 7/25 → cos²α = 1
– sen²α = 1 – (7/25)² = (625 – 49)/625
→ cosα = ± 24/25
→ cosα = +24/25, (0 < α < π/2, 1º quadrante)
cosβ
= 4/5 → sen²β = 1 – cos²β = 1 – (4/5)² = 9/25
→ sen²β = ± 3/5 → senβ = ─ 3/5, (3π/2 < β < 2π, 4º quadrante)
Logo,
sen(α – β) = senα.cosβ – senβ.cosα =
= 7/25*4/5 ─ (─ 3/5)*24/25 =
= 28/125 + 72/125
= 100/125 = 4.25/5.25 = 4/5
Resposta: sen(α
– β) = senα.cosβ
– senβ.cosα
= 4/5
Observação: (OUTRA MANEIRA DE RESOLVER
COM MAIS RAPIDEZ)
É lembrar dos Ternos do Triângulo de Pitágoras.
E perceber
que:
EX-05
Calcular sen(π/12).
Solução:
sen(π/12)
= sen(π/3 –
π/4) =
= sen(π/3).cos(π/4)
– sen(π/4). cos(π/3) =
Resposta: (√6 – √2)/4
EX-06
Reduzir ao
máximo a expressão:
Solução:
y = [cos(π/4).cos(x) ─ sen(π/4).sen(x)] +
[cos(π/4).cos(x)
+
sen(π/4).sen(x)] = 2. cos(π/4).cos(x) = 2.√2/2.cos(x) = √2.cos(x)
Resposta:
√2.cos(x)
EX-07
Calcular o
valor de:
y = cos 25º. cos 35º ─ sen 25º.sen 35º
Solução:
cos 25º.cos 35º ─ sen 25º.sen 35º = cos (25º + 35º) =
= cos 60º = 1/2
Resposta: 1/2
EX-08
Demonstrar a
seguinte igualdade:
Solução:
EX-09
Sendo (a + b =
π/4), determinar o valor de y:
y=[cos(a) + sen(b)]² + [sen(a) + cos(b)]²
Solução:
y=[cos(a)
+ sen(b)]² + [sen(a) +
cos(b)]² =
=cos²(a)+2cos(a)sen(b)+sen²(b)+
+sen²(a)+2sen(a)cos(b)+cos²(b)=
= [cos²(a)+sen²(a)]+[sen²(b)+cos²(b)]+
+2cos(a)sen(b)+2sen(a)cos(b)=
= 2 + 2cos(a)sen(b)+2sen(a)cos(b)=
= 2 + 2 [cos(a)sen(b) + sen(a)cos(b)]
= 2 + 2.[sen(b).cos(a) + sen(a)cos(b)] =
= 2
+ 2.sen (b+a)= 2 + √2/2 =
= 2 + √2
Resposta: y = 2 + √2
Observação:
EX-10
Verificar a
identidade:
cos(x + y).cos(x – y) = cos²x – sen²y = cos²y – sen²x
Solução:
cos(x + y).cos(x –
y) =
= (cosx.cosy – senx.seny).( cosx.cosy + senx.seny) =
= (cosx.cosy)² ─ (senx.seny)² = cos²x.cos²y ─
sen²x.sen²y =
sen²y + cos²y = 1 → (cos²y
= 1 – sen²y)
= cos²x.(1 – sen²y) – sen²x.sen²y =
= cos²x – cos²x.sen²y - sen²x.sen²y =
= cos²x – sen²y.(cos²x+sen²x) = cos²x – sen²y
sen²y + cos²y = 1 → (sen²y
= 1 – cos²y)
= cos²x.cos²y ─ sen²x.(1 – cos²y) =
= cos²x.cos²y – sen²x + sen²x.cos²y) =
= cos²y.(cos²x+sen²x) – sen²x = cos²y – sen²x
EX-11
Dados cotg(α) = 3/4 e cos(β) = √2/10, β do 1º quadrante, calcular tg(α + β).
Solução:
cotg(α) = 3/4 → tg(α) = 1/cotg(α)
→ tg(α) = 4/3
Como β está no 1º quadrante:
sen(β) = +(7√2)/10
Então temos:
EX-12
Satisfeita as
condições de existência verifique a seguinte identidade:
Solução:
EX-13
Demonstrar que
cotg(x + y) em função de cotg(x) e cotg(y) é:
Solução:
(dividindo o dividendo e o divisor por [sen(y).sen(x)], tem-se ).
EX-14
Supondo
satisfeitas as condições de existência, provar que:
Prova:
EX-15
Calcular o
valor de y da seguinte expressão:
Solução:
Resposta: y=1




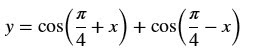










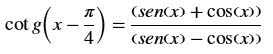



Nenhum comentário:
Postar um comentário