EX-01
O mostrador do relógio de uma torre é dividido em 12 partes
iguais (horas), cada uma das quais é subdividida em outras 5 partes iguais
(minutos). Se o ponteiro das horas (OB) mede 70cm e o ponteiro dos
minutos (OA) mede 1m, qual será a
distância AB , em função do ângulo entre os ponteiros, quando o relógio marcar 1 horas e 12 minutos?
Solução:
Quando o relógio marca exatos 1 hora, o ângulo entre os
ponteiros (menor e maior) é 30º. Portanto, o houve um deslocamento de 30º do
ponteiro pequeno em relação à nossa referência indicado na figura.
Quando
o ponteiro grande (minutos) chega à marca de 12 minutos, ele terá se deslocado:
Enquanto que, durante os mesmos 12 minutos, o ponteiro
pequeno (horas) andou de y graus:
Resumindo:
O ponteiro grande andou: 72º
O ponteiro pequeno andou: 30 + 6 = 36º
Portanto, o ângulo formado entre os ponteiros às 1 hora e 12
minutos é:
xº = 72 – 36 = 36º
Podemos observar que temos um triângulo AOB,
sendo que o lado AB está oposto ao ângulo formado entre os ponteiros. Logo para
calcular o valor do lado AB, basta aplicar a lei dos cossenos:
Reposta:
A distância AB = 6 metros
EX-02
Sejam
A, B, C e N quatro pontos em um mesmo plano,
conforme mostra a figura a seguir:
a) Calcule o raio da circunferência que
passa pelos pontos A, B e N.
b) Calcule o comprimento do segmento NB.
Solução:
a) Tomando o ∆ANB e aplicando a lei dos senos,
tem-se:
b) No triângulo ∆BCN, retângulo em N, tem-se:
No triângulo ∆ANB a soma dos
ângulos internos é 180º, logo:
Portanto, pela lei dos senos:
Obtivemos que:
EX-03 (UNICAMP)
Na figura abaixo, ABC e BDE são triângulos isósceles
semelhantes de bases 2a e a, respectivamente, e o ângulo CÂB = 30º. Determinar o comprimento do segmento CE.
Solução:
Completando o desenho com os dados informados e preparando
convenientemente, para os cálculos:
∆BCP:
Aplicando a Lei dos Senos para calcular o lado BC:
Como o ∆BEQ possui metade das dimensões
do ∆BCP:
∆BCE:
Aplicando a Lei dos Cossenos para calcular o segmento CE:
EX-04 (ITA-2011)
Num triângulo AOB o ângulo AÔB mede 135° e
os lados AB e OB medem √2 cm e √( 2 - √3) cm, respectivamente. A circunferência
de centro em O e raio igual à medida de OB intercepta AB no ponto C (≠ B).
a) Mostre que OÂB mede 15°.
b) Calcule o
comprimento de AC
Solução:
a) Aplicando a lei
dos senos ao ∆ABO, temos:
Vamos calcular o
sen(15º):
Elevando ambos os
membros por 2, temos:
Portanto,
está provado que o ângulo α = 15º → OÂB
= 15º
b) Soma dos ângulos
internos do triângulo ∆ABO, temos:
O triângulo ∆OCB é
isósceles e sabemos que:
Pela soma dos
ângulos internos, temos:
Este resultado
implica que o triângulo ∆ACO é também isósceles, pois o ângulo AÔC = 135º - CÔB
= 135º - 120º = 15º, logo, OÂC = AÔC = 15º.
Portanto,
EX-05 (UNESP 2013)
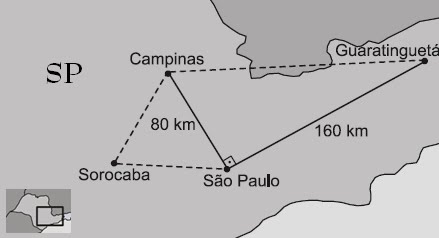
Um professor de geografia forneceu a seus alunos um mapa do
estado de São Paulo, que informava que as distâncias aproximadas em linha reta
entre os pontos que representam as cidades de São Paulo e Campinas e entre os
pontos que representam as cidades de São Paulo e Guaratinguetá eram,
respectivamente, 80 Km
e 160 Km .
Um dos alunos observou, então, que as distâncias em linha reta entre os pontos
que representam as cidades de São Paulo, Campinas e Sorocaba formavam um
triângulo equilátero. Já um outro aluno notou que as distâncias em linha reta
entre os pontos que representam as cidades de São Paulo, Guaratinguetá e
Campinas formavam um triângulo retângulo, conforme mostra o mapa.
Com essas informações, os alunos determinaram a distância
(em KM), em linha reta entre os pontos que representam as cidades de
Guaratinguetá e Sorocaba.
Solução:
O triângulo ∆KCS é equilátero, portanto temos:
Logo, o ângulo KSG
no triângulo ∆KSG é igual à:
Aplicando a lei dos
cossenos no triângulo ∆KSG, temos:
EX-06 (FUVEST 2011)
No losango ABCD de lado 1, representado na figura, tem-se
que M é o ponto médio de AB, N é o ponto médio de BC e MN = √14/4.
Calcular a distância DM.
Solução:
Aplicando a lei dos
cossenos no triangulo ∆BMN, temos:
Observamos que
(α+β) = 180º, portanto, são suplementares; logo:
E o ângulo β = DÂM no triângulo ∆ADM
Aplicando,
novamente, a lei dos cossenos no triângulo ∆ADM,
temos:
EX-07
Um grupo de escoteiros pretende escalar uma montanha até o
topo, representado na figura abaixo pelo ponto D, visto sob ângulos de 40º do
acampamento B e de 60º do acampamento A. Dado: sen20º=0,342
Considerando que o
percurso de 160 m
entre A e B e realizando segundo um ângulo de 30º em relação à base da
montanha, então, determine a distância entre B e D, em m.
Solução:
Colocando os dados
na figura, temos:
Aplicando a lei dos
senos no triângulo ∆ABD, temos:
EX-08
A figura abaixo apresenta um prisma reto cujas bases são
hexágonos regulares. Os lados dos hexágonos medem 5 cm cada um e a altura do
prisma mede 10 cm .
a) Calcule o volume do prisma.
b) Encontre a área da secção desse prisma pelo plano que
passa pelos pontos A, C e A’.
Solução:
a) O volume do
prisma é dado pelo produto entre a área do polígono da base e a sua altura. Assim,
o seu volume V, em centímetros cúbicos, é tal que:
O polígono da base é um hexágono regular. Relembrando o calculo de área de um hexágono:
Logo, volume do prisma é:
b) A secção desse
prisma pelo plano α, que passa pelos
pontos A, C e A’, é o retângulo ACC’A’, cuja altura AA’ mede 10 cm e cuja base CA pode ser
calculada da seguinte maneira:
Aplicando
a leis dos cossenos:
Logo, a área da secção é:
EX-09
Um satélite orbita a 6.400 km da superfície da
Terra. A figura abaixo representa uma seção plana que inclui o satélite, o
centro da Terra e o arco de circunferência AB. Nos pontos desse arco o sinal do
satélite pode ser captado. Responda às questões abaixo, considerando que o raio
da Terra também mede 6.400
km .
a) Qual o comprimento do arco AB indicado na figura?
b) Suponha que o ponto C
da figura seja tal que cosθ
= 3/4. Determine a distância d entre
o ponto C e o satélite.
Solução:
Seja x o
comprimento do arco AB, então:
b) Aplicando a lei dos cossenos ao triângulo ∆COS,
tem-se:
EX-10
Calcular os lados b e c de um triângulo ABC no qual a = 10, ângulo B = 30º e ângulo C = 45º.
Solução:
Aplicando a lei dos senos no triângulo ABC:

































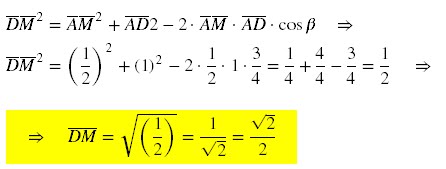
















bom muito bom
ResponderExcluirObrigada!
ResponderExcluir