1)
FEBA
Sabe-se que -1 é uma das raízes da equação: x² -
5x + 3m = 0. O valor de m² é:
a) 4 b)
9 c) 16 d) 36
e) 42
2)
Para
que valores reais da constante m a equação 2x² - mx + 8 = 0 admite duas raízes
reais e iguais?
3)
Para
que valores reais da constante m a equação x² - 6x + m = 0 admite raízes reais
e distintas?
4)
Para
que valores reais da constante m a equação mx² - 2mx + m + 1 = 0 não admite
raízes reais?
5)
Qual
é, respectivamente, a soma e o produto das raízes das equações a seguir:
a)
x² - 3x – 4 = 0
b)
x² - 5x + 6 = 0
c)
2x² - 7x – 2 = 0
d)
5x² - 10x +1 = 0
6)
Sendo
x’ e x’’ as raízes da equação 2x² - 6x – 3 = 0 , obtenha: (tente resolver este
exercício sem encontrar x’ e x’’ separadamente)
a) x’
+ x’’
b) x’
. x’’
c)
(x’)².x’’ + x’.(x’’)²
d)
1/x’ + 1/x’’
e)
(x’)² + (x’’)²
7)
Para
que a soma das raízes da equação (k - 2)x² - 3kx + 1 = 0 seja igual ao seu
produto devemos ter:
8)
Na
equação do 2º grau ax² + bx + c = 0 , os números a e c têm sinais contrários. Pode-se
afirmar que:
a) A
equação tem duas raízes reais de sinais contrários
b) A
equação tem duas raízes reais e positivas
c) A
equação tem duas raízes reais e negativas
d) A
equação pode não ter raízes reais.
9)
O
valor real de m para que uma das raízes da equação x² + mx + 27 = 0 seja o
quadrado da outra é:
a) 0 b) -3 c) -6 d) -9 e) -12
10)
CESGRANRIO
Se m
e n são as raízes da equação 7x² + 9x + 21 = 0, então (m + 7).(n + 7) vale:
a) 49
b) 43 c) 37 d) 30 e) 30/7
11)
Um
pai tinha 36 anos quando nasceu seu filho. Multiplicando-se as idades que
possuem hoje, obtêm-se um produto que é igual a 4 vezes o quadrado da idade do
filho. Hoje, as idades do pai e do filho são, respectivamente,
a) 44
e 11 b) 48 e 12 c) 52 e 13
d) 60 e 15 e) 56 e 14
12)
UNICAMP
Ache
dois números inteiros, positivos e consecutivos, sabendo que a soma de seus
quadrados é 481.
13)
PUC
Sendo
x’ e x’’ os zeros ou raízes da função quadrática f(x) = x2 - 8x + m,
determinar m para que se tenha 3x’ – 4x’’ = 3.
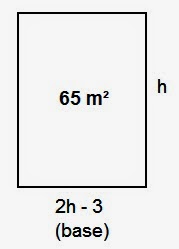
14)
Num
retângulo, cuja área é 65 m2 ,
a base é 3m menor que o dobro da sua altura. Obtenha sua base.
15)
FUVEST
O conjunto-verdade da equação
Gabarito:
1.
a
2.
8, -8
3.
m < 9
4.
m > 0
5.
a) soma=3, produto=-4
b) soma=5, produto=6
c) soma=7/2, produto=-1
d) soma=2, produto=1/5
6.
a) 3
b) -3/2
c) -9/2
d) -2
e) 12
7.
c
8.
a
9.
e
10. b
11. b
12. 15 e
16
13. m=15
14. 10 m
15. e
Soluções:
1. x =
-1 é raiz
x² - 5x + 3m = 0,
m²=?
(-1)² - 5(-1) + 3m = 0 ↔ 6 + 3m = 0 ↔ m = -2 →
m² = 4
2. 2x² -
mx + 8 = 0
Para que tenhamos 2 raízes iguais: ∆ = b² - 4ac = 0
Logo:
∆ =
(-m)² - 4.2.8 = m² - 64
∆ = 0 ↔ m² - 64 = 0 ↔ m = ± 8
3. x² -
6x + m =0; m = ?
Para que tenhamos 2 raízes reais e distintas:
∆ = b²
- 4ac > 0
∆ =
(-6)² - 4.1.m = 36 – 4m
∆ > 0 ↔ 36 – 4m > 0 ↔ - 4m > - 36 ↔ m < 9
4. mx² -
2mx + m + 1 = 0; m = ?
∆ < 0
para que não tenhamos raízes reais.
∆ = b²
- 4ac = (-2m)² -4.m.(m+1) =
= 4m² - 4m² - 4m = - 4m
∆ < 0 ↔ -4m < 0 ↔ m > 0
5. a) x²
- 3x – 4 = 0
Seja a equação genérica ax²+bx + c = 0 e x’ e x’’
raízes desta. Assim vale as seguintes
relações entre os coeficientes e raízes:
Soma das
raízes: x’ + x’’ = -b/a
Produto das
raízes: x’.x’’ = c/a
Portanto:
soma das raízes = 3; produto das raízes = -4
b) x² -
5x + 6 = 0
Soma = 5
Produto =
6
c) 2x² -
7x - 2 = 0 → x² - (7/2)x – 1 = 0
Soma =
7/2
Produto =
-1
d) 5x² -
10x + 1 = 0 → x² -
2x + 1/5 = 0
Soma = 2
Produto =
1/5
6. 2x² -
6x – 3 = 0
Seja x’
e x’’ raízes da equação.
a) x’ + x’’ = 6/2 = 3
b) x’. x’’ = -3/2
c) (x’)².x’’ + x’.(x’’)² = x’.x’’.(x’ + x’’) =
= -(3/2).3 = -9/2
d) 1/x’ + 1/x’’ = (x’’ + x’)/x’.x’’ = 3/(-3/2) =
= 3.(-2/3) = - 2
e) (x’)² + (x’’)² =
(x’ +
x’’)² = (x’)² +2.x’.x’’ + (x’’)² →
(x’ + x’’)² - 2.x’.x’’ = (x’)² + (x’’)² →
3² - 2.(-3/2) = (x’)² + (x’’)² →
(x’)² +
(x’’)² = 9 + 3 = 12
7.
k = ?
; (k - 2)x² - 3kx + 1 = 0
Para que tenhamos a soma das raízes seja igual ao
produto.
1/(k – 2) = 3k/(k – 2) ↔ 1 = 3k ↔ k = 1/3
8. ax² +
bx + c = 0; a e c têm sinais contrários.
Bhaskara:
∆ = b² - 4ac (como a e c têm sinais contrários), b² - 4ac > 0, logo a equação dada possui sempre 2
raízes reais e diferentes.
Portanto, a equação sempre tem 2 raízes reais de
sinais contrários.
9.
m =
?, x² + mx +27 = 0
Para que x’, (x’)² sejam as raízes.
Soma das raízes = -m = x’ + (x’)²
Produto das raízes = 27 = x’.(x’)² = (x’)³ ↔ x’ = 3
Como -m = x’ + (x’)² = 3 + (3)² = 12 ↔ m = - 12
(m + 7).(n + 7) = ?
(x-m).(x-n)
= 0 ↔ x² - (m+n).x + m.n = 0
Por
comparação temos que:
m + n = -9/7 e m.n = 21/7 = 3
Portanto,
(m + 7).(n + 7) = m.n +
7.(m + n) + 49 =
3 +
7.(-9/7) + 49 = 3 – 9 + 49 = 43
11. Considerando a idade do filho de x:
(36 + x).x = 4.x² ↔ 36x + x² = 4.x² ↔
-3x²
+ 36x = 0
3x² - 36x = 0 ↔ x² - 12x = 0 ↔ x(x
– 12) = 0 ↔
x = 0, ou x = 12 (não pode ser zero).
Portanto, x = 12 (= idade do filho)
Logo a idade do pai = 36 + x = 36 + 12 = 48
x² + (x + 1)² = 481
x² + x² +2x + 1 = 481 ↔ 2x² + 2x – 480 = 0 ↔
x² + x - 240 = 0 ↔
(x+16).(x-15) = 0 ↔
x=-16, x=15
Como x é positivo: x = 15, x+1 = 16
13. x’ e x’’ são raízes da equação x² - 8x + m =
0
m = ?
para 3x’ – 4x’’ = 3
Vamos determinar as raízes x’ e x’’ por
Bhaskara:
∆ = b²
- 4ac = (-8)² - 4.1.m = 64 – 4m = 4(16 – m)
x’ = (-b+√∆)/2a = [-(-8) +
√4(16-m)]/2 = [8 + 2√(16-m)]/2 =
4 + √(16-m)
x’’ = (-b-√∆)/2a
= [-(-8) - √4(16-m)]/2 = [8 - 2√(16-m)]/2 =
4 - √(16-m)
Então,
3x’ – 4x’’ = 3 ↔ 3.[ 4 +
√(16-m)] – 4.[ 4 - √(16-m)] = 3
↔ 12 + 3√(16-m) – 16 + 4√(16-m) = 3 ↔ 7√(16-m) = 7 ↔
√(16-m) = 1 ↔ 16-m = 1↔
-m = -15 ↔ m = 15
14.
(2h-3).h = 65 ↔ 2h²
- 3h – 65 = 0 ↔
(h+5).(h-13/2) = 0
H não pode ser negativo porque é altura,
logo:
h = 13/2
base = 2h – 3 = 2. 13/2 – 3 = 13 – 3 = 10
m
15.
[(x-2).(x+2) + 2.2]/2.(x-2) = - (x-2)/2.(x-2)
[(x-2).(x+2) + 2.2 + (x-2)]/2.(x-2) = 0
x ≠ 2,
porque não pode dividir por zero;
(x-2).(x+2) + 2.2 + (x-2) = 0
X² - 4 + 4 + x – 2 = 0 ↔ x² + x – 2 = 0 ↔
(x+2).(x-1)=0
Portanto,
x = -2, ou x = 1






Nenhum comentário:
Postar um comentário