1)
EX-01
André, Bento e Carlos têm, juntos, 41 anos. Calcular as
idades de
cada um sabendo que Bento é três anos mais velho que André e
Carlos é quatro anos mais jovem que André.
2)
EX-02 (FUVEST)
São dados três números naturais a, b e c, com a < b <
c.
Sabe-se que o maior deles é a soma dos outros dois e o menor
é um
quarto do maior. Se a – b + c = 30, então o valor de a + b +
c será:
a) 45 b) 60 c)
900 d) 120 e) 150
3)
EX-03 (UNIFOR)
Um grupo de amigos comprou um presente por R$ 6300,00.
Pretendiam dividir essa quantia entre si, em partes iguais. Como 2 membros do
grupo não puderam cumprir o compromisso, cada um dos restantes teve sua parcela
aumentada de R$ 360,00. O número de pessoas do grupo era, inicialmente,
a) 11 b) 10 c)
9 d) 8 e)
7
4)
EX-04 (UNICAMP)
O IBGE contratou um certo número de entrevistadores para
realizar o recenseamento em uma cidade. Se cada um deles recenseasse 100
residências, 60 delas não seriam visitadas. Como, no entanto, todas as
residências foram visitadas e cada recenseador visitou 102, quantas residências
têm a cidade?
5)
EX-05 (UNI-RIO)
Num escritório de advocacia, trabalham apenas dois advogados
e uma secretária. Como o Dr. André e o Dr. Carlos sempre advogam em causas
diferentes, a secretária, Cláudia, coloca 1 grampo em cada processo do Dr.
André e 2 grampos em cada processo do Dr. Carlos, para diferenciá-los
facilmente no arquivo. Sabendo-se que, ao todo, são 78 processos nos quais
foram usados 110 grampos, podemos concluir que o número de processos do Dr. Carlos
é igual a:
a) 64 b) 46 c) 40 d) 32 e)
28
6)
EX-06 (UNICAMP)
Um copo cheio de água pesa 385g; com 2/3 da água pesa 310g.
Pergunta-se:
a) Qual é o peso do copo vazio?
b) Qual é o peso do copo com 3/5 de água?
7)
EX-07
Considere o sistema não-linear abaixo:
Então, o valor de x2 + y 2 é:
8)
EX-08
Resolver, em RxR
, o seguinte sistema não-linear
9)
EX-09
Resolver em R as
equações abaixo:
10)
EX-010
Resolver em R as
seguintes equações:
Gabarito
1. André tem 14 anos, Bento
tem 17 anos e Carlos tem 10 anos.
2. d
3. e
4. 3060
5. d
6. a) 160g
b) 295g
7. d
8. V = {(28; 10); (4; -2)}
Soluções
1)
EX-01- Solução
Colocando
as informações na tabela, temos que:
x + (x +3) + (x – 4) = 41 → 3x =
42 → x = 14
Logo:
André = 14 anos
Bento = 17 anos
Carlos = 10 anos
2)
EX-02- Solução
c = a + b (I)
a = c/4 (II)
a – b + c = 30 (III)
(I) c = a + b → a = c – b = - b + c → a = - b +c
Em (III)
(-b + c) – b + c = 30 → 2c – 2b = 30 → c – b = 15
Então,
a = c – b = 15
(II) a = c/4 → c = 4a → c = 60
(III) a – b + c = 30
(I) c = a + b → b = c – a =
60 – 15 = 45
Logo,
a + b + c = 15 + 45 + 60 =
120
3)
EX-03- Solução
x = número de amigos inicial
y = parcela de cada um =
6300/x
6300/(x-2) = y + 360
6300/(x-2) = 6300/x + 360 → 6300/(x-2) = 6300/x + 360x/x
6300/(x-2) = (6300 + 360x)/x → 6300x = (6300+360x)(x-2)
6300x = 6300x -2*6300 + 360x² - 2*360x → 360x² -2*360x -2*6300
x² - 2x – 35 = 0 → (x-7)(x+5)
= 0 ↔ x=7, ou x=-5
Portanto,
O número inicial de amigos é:
7
4)
EX-04- Solução
x = número de entrevistadores
y = número de residências
100x + 60 = y
102x = y
Igualando as duas equações:
100x + 60 = 102x → 2x = 60 →
x = 30 (entrevistadores)
Então,
y = 102x = 102*30 = 3060 → y
= 3060
5)
EX-05- Solução
x = processos André
y = processos Carlos
x + y = 78, (total de processos)
x + 2y = 110, (total de grampos)
Temos um sistema de equações:
Como
quero saber quanto é o valor de y (=processos de Carlos), vamos subtrair membro
a membro da seguinte forma:
6)
EX-06- Solução
x = peso do copo
y = peso da água (100%)
Peso do copo = x = 385 – y =
385 – 225 = 160 g
Peso do copo com 3/5 de água
= x + (3/5)y = 160 + (3/5)*225 =
= 295 g
7)
EX-07- Solução
Elevando ambos os membros da
equação x-y = 1, temos
(x-y)² = 1² → x² - 2xy + y² =
1 → x² + y² = 1 + 2xy
De outra equação dada: xy =
15/4
Logo: x² + y² = 1 + 2xy = 1 +2.15/4 = 17/2 → x² + y² = 17/2
8)
EX-08- Solução
y² - 8y – 20 = 0 → (y-10)(y+2) = 0 ↔
y=10, ou y = -2
y=10 → x = 8 + 2y = 8 + 2*10 = 28 → x = 28
y=-2 → x= 8 + 2*(-2) = 4 → x = 4
9)
EX-09- Solução
Existem várias maneiras de
resolver as equações de 2º grau.
Por fatoração:
a) x² - 5x + 6 = 0 →
(x-2)(x-3) = 0 → x’=2, x’’=3
b) 6x² - x – 1 = 0
Por Bhaskara:
x = (-b ± √∆)/2a
∆ = b²-4ac = 1-4*6*(-1) =
1+24 = 25
x’ = [-(-1) +5]/12 = 6/12 =
1/2
x’’ = [-(-1) -5]/12 = -4/12 =
-1/3
c) x² + 4x +3 =0
Por fatoração:
x² + 4x + 3 = (x+1)(x+3) = 0
↔ x’ = -1, x’’= -3
d) 6x² -13x + 6 = 0
Por Bhaskara:
∆ = b² - 4ac = 13² - 4*6*6 =
25 → √∆ = 5
x’ = [-(-13) + 5]/2*6 = 18/12
= 3/2 → x’ = 3/2
x’’ = [-(-13) – 5]/2*6 = 8/12
= 2/3 → x’’ = 2/3
e) 4x² - 12x + 9 = 0
Por Bhaskara:
∆ = b² - 4ac = (-12)² - 4*4*9
= 0
x’ = x’’ = [-(-12)+0]/2*4 =
12/8 = 3/2 → x = 3/2
f) x² + 4x + 4 = 0
Por fatoração:
(x+2).(x+2) = 0 → (x + 2)² =
0 → x = -2
g) 4x² - 4x + 2 = 0
Por Bhaskara:
∆ = b² - 4ac = (-4)² - 4*4*2
= 16 – 32 = - 16
Como ∆ é negativo, não existem
raízes no campo R (reais)
h) x² - 2x + 5 = 0
Por Bhascara:
∆ = b² - 4ac = (-2)² - 4*1*2
= 4 – 8 = - 4
Como ∆ é negativo, não
existem raízes no campo R (reais)
10)
EX-10- Solução
a) x² + 9 = 0 → x² = - 9
Não existe em R um número que
elevado a dois resulte em um número negativo.
b) x² - 9 = 0 → x² = 9 → x =
± √9 → x = ± 3
c) 2x² - 5x = 0 → x(2x-5) = 0
↔ x = 0, 2x-5 = 0
2x – 5 = 0 → x = 5/2
d) x.x = 7x → x.x – 7x = 0 →
x(x-7) = 0 ↔ x = 0, x = 7
e) 3x² - 3 = 0 → x² - 1 = 0 →
x² = 1 → x = ± 1
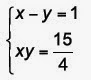









Nenhum comentário:
Postar um comentário