EX-01 (FUVEST 2010)
Sejam x e y dois números reais, com 0 < x <π/2 e π/2 < y < π, satisfazendo seny = 4/5 e 11 sen x + 5 cos(y –
x) = 3. Nessas condições, determine
a) cos y
b) sen 2x
Solução
Então,
Logo:
Pois, ( π/2
< y < π) o y está no 2º
quadrante.
b)
Calculando o senx, da identidade fundamental da
trigonometria:
Como 0<x<π/2,
então senx não pode ser zero, logo: senx = 5/13.
Portanto,
Temos todos os dados para calcular sen 2x:
EX-02 (FUVEST 2009)
Seja x no intervalo ] 0, π/2 [ satisfazendo a equação tgx + (2/√5)*secx = 3/2. Assim,
calcule o valor de:
a) secx
b) sen(x+π/4)
Solução
a)
Elevando ambos os membros por 2, temos:
De identidade fundamental da trigonometria, temos:
Igualando as equações (1) e (2), temos:
Aplicando Báskara, temos:
b)
Temos adição de arcos, então sabemos que:
Então,
Temos que calcular os valores de senx e cosx.
De resultado do item anterior, podemos calcular o valor do
cosx:
De identidade fundamental da trigonometria, temos o valor de
senx:
Agora temos todos os valores para responder o item b:
EX-03 (FUVEST 2008)
A medida x, em radianos, de um ângulo satisfaz π/2 < x < π e verifica a equação senx + sen2x +
sen3x = 0. Assim,
a) determine x;
b) calcule cosx + cos2x + cos3x.
Solução
b)
EX-04 (FUVEST 2007)
Um arco x está no terceiro quadrante do círculo
trigonométrico e verifica a equação 5cos2x+3senx=4. Determine os valores de senx e cosx.
Solução
De identidade fundamental da trigonometria, temos o valor de
cosx:
EX-05 (FUVEST 2005)
Determine todos os valores de x pertencentes aos intervalos
[0, 2π] que satisfazem a
equação cos²2x = ½ - sen²x.
Solução
Aplicando Báskara para resolver a equação do segundo grau,
temos
Determinando todos os valores de x no intervalo [0, 2π]:
y1 = 1/2
y2 = 1/4
Resposta:
EX-06 (FUVEST 2003)
Determine os valores de x no intervalo ]0,2π[ para os quais cosx ≥ √3.senx+ √3.
Solução
Reescrevendo e aplicando o conceito de adição de arcos,
temos:
Visualizando no círculo trigonométrico, onde k é inteiro, temos:
Então podemos escrever que:
Do enunciado temos que (0 < x < 2π), sendo assim k = 1. Portanto,
tem-se:
Resposta:
EX-07 (FUVEST 2002)
Determine as soluções da equação (2cos²x + 3senx)(cos²x –
sen²x) = 0 que estão no intervalo [0, 2π].
Solução
Resolvendo a equação (1), temos:
Resolvendo a equação (2), temos:
Resposta:
EX-08 (FUVEST 2001)
a) Calcule cos3θ
em função de senθ e cosθ
b) Calcule sen3θ
em função de senθ e cosθ
c) Para 0 < θ
< π/2, resolva a equação
sen²θ + 1/2.cosθ + 1 = sen3θ/senθ – cos3θ/cosθ
Solução
a)
b)
c)
EX-09 (FUVEST 2000)
Determine os números reais x e y, com 0 ≤ x +y ≤ 2π e 0 ≤ y ≤ π, tais que
Solução
De segunda equação do sistema de equações apresentado,
temos:
De primeira equação do sistema e algumas manipulações para
obter o cos²x, temos:
(2) em (1), temos:
Aplicando Báskara, temos:
Calculando os valores de x:





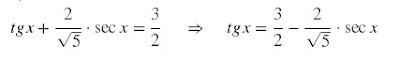
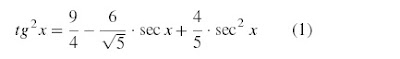



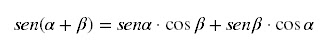






















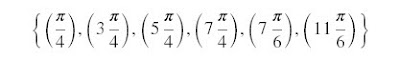









mt bom
ResponderExcluir