1)
Na figura abaixo, calcule o valor da medida x.
Solução:
A soma dos ângulos internos de um triângulo é sempre 180º,
portanto, o ângulo no vértice C = 180 – (105 + 45) = 30º
Pela lei dos senos tem-se:
x/sen45º =
100/sen30º → x/(√2/2) = 100/(1/2) → x = 100.√2
2)
No
triângulo abaixo, determine as medidas de x e y, sabendo-se que
Solução:
A soma dos ângulos internos de um triângulo é sempre 180º,
portanto, o ângulo no vértice C = 180 – (135 + 15) = 30º
Pela lei dos senos tem-se:
x/sen135º = y/sen15º = √2/sen30º
Sabemos que:
1)
sen135º = sen45º = √2/2,
2) sen15º = sen(45º- 30º) = sen45.cos30
– cos45.sen30 =
= √2/2*√3/2 - √2/2*1/2 = (√6 - √2)/4
Logo:
x/sen135º =
√2/sen30º → x/(√2/2) = √2/(1/2) → x = 2
y/sen15º =
√2/sen30º → y = √2*sen15º/sen30º → y = [√2*(√6
- √2)/4]/(1/2)
→ y = (√12
– 2)/2 →
y = 2(√3 – 1)/2 → y = (√3 – 1)
3)
Uma ponte deve ser construída sobre um rio, unindo os pontos
A e B, como ilustrado na figura a seguir. Para calcular o comprimento AB,
escolhe-se um ponto C, na mesma margem em que B está, e medem-se os ângulos CBA
= 57° e ACB = 59°. Sabendo que BC mede 30m, calcule, em metros, a
distância AB . (Dado: use as
aproximações sen(59°) ≈ 0,87 e sen(64°) ≈ 0,90)
Solução:
A soma dos ângulos internos de um triângulo é sempre 180º,
portanto, o ângulo no vértice A = 180 – (57 + 59) = 64º
Aplicando a lei dos senos, tem-se:
BC/sen64º = AB/sen59º →
AB = BC*sen59º/sen64º = 30*0,87/0,90 ≈ 29
Portanto, a distância AB = 29
metros
4) FUVEST
No quadrilátero a seguir, BC = CD = 3 cm , AB = 2 cm , ângulo ADC = 60° e ângulo ABC = 90°.
Qual é a medida, em cm, do perímetro do quadrilátero?
Solução:
O lado AC no triângulo ABC é : AC = √13
Vamos determinar o segmento AD = x
Aplicando Lei dos Cossenos no vértice D do triângulo ACD:
(√13)² = x² + 3² - 2.x.3.cos60º → 13 =
x² + 9 – 3x → x² - 3x – 4 = 0 →
(x – 4).(x + 1) = 0 ↔
x = 4, ou x = -1 (x deve ser positivo e diferente de zero).
Portanto, x
= 4
Logo,
o perímetro do quadrilátero é igual a: p = 2 + 3 + 3 + 4 = 12 → p = 12 cm
5) FUVEST
Na figura abaixo, tem-se AC = 3, AB = 4 e BC = 6. Qual é o
valor de CD?
Solução:
Primeira opção: (aplicando trigonometria)
cosC = x/3 e
c² = b² + a² -2.a.b.cosC
→
4² = 3² + 6² - 2.3.6. cosC → cosC
= 29/36,
Logo:
x/3 = 29/36 → x = 29/12
Segunda opção: (aplicando Teorema de Pitágoras)
∆ABD: 4² = y² + (6-x)² → 16 = y² + 36 -12x +x² → x² + y² = - 20 +
12x
∆ACD: x² + y² = 9
Portanto, tem-se: 9
= - 20 + 12x → x = 29/12
6) FUVEST
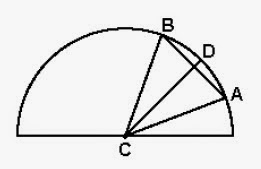
Em uma semi-circunferência de centro C e raio R, inscreve-se
um triângulo equilátero ABC. Seja D o ponto onde a bissetriz do ângulo ACB
intercepta a semicircunferência. Determine o comprimento da corda AD.
Solução:
∆ABC é eqüilátero, logo: m(BAC) = m(ABC) = m(BCA) = 60º
Como CD é bissetriz do ângulo ACB, então m(ACD) = 30º.
∆ACD é triângulo (isósceles) de cujos lados CA = CD = R.
Aplicando a lei dos cossenos temos que:
AD² = CA² +
CB² - 2. CA.CB.cos30º → AD² = R² + R² -
2.R.R.√3/2 →
AD² = 2R² - 2.R².√3/2 = 2R² - R².√3 = R².(2 - √3) →
AD² = R²(2 - √3) → AD = R.√(2-√3) →
7) FUVEST
As páginas de um livro medem 1dm de base e
 dm de altura.
dm de altura.
Se este livro foi parcialmente aberto, de tal forma que o
ângulo entre duas páginas seja 60°, determine a medida do ângulo α, formado
pelas diagonais das páginas.
Solução:
∆BCD é eqüilátero porque o ângulo D = 60º e os lados DC = BD
= 1
Então, o lado BC = 1
∆ABC é isósceles (lados iguais aos diagonais das páginas e
de base BC = 1).
Determinando o valor das diagonais, por teorema de
Pitágoras:
AC² = 1² + [√(1+√3)]²
= 1 + 1 + √3 = 2 + √3 → AC = √[2 + √3] = AB
Aplicando a lei dos cossenos ao triângulo ABC, temos:
BC² = AC² + AB² - 2.AC.AB.cosα
1² = {√[2 + √3]}² + {√[2
+ √3]}² - 2. {√[2 + √3]}. {√[2 + √3]}.cosα
1 = 2.(2 + √3) – 2.( 2 + √3).cosα
Então,
O ângulo α cujo cosseno é √3/2 = 30º → α = 30º
8) FUVEST
Um triângulo T tem lados iguais a 4, 5 e 6. Determine o
co-seno do maior ângulo de T.
Solução:
O maior ângulo é Â
Aplicando a lei dos cossenos, temos:
6² = 4² + 5² - 2.4.5.cosÂ
→ 36 = 16 + 25 – 40.cos → - 5
= - 40.cosÂ
cos = 5/40 = 1/8
→ cos = 1/8
9)
Dado o triângulo ABC e sabendo que o lado a mede 16, o lado b mede 10 e o ângulo formado por estes lados é 60º, qual é o valor
do lado c do triângulo?
Solução:
Aplicando a lei dos cossenos em relação ao vértice C:
c² = 10² + 16² - 2.10.16.cos60º → c² =
100 + 256 – 160 = 196 →
c² = 196 → c = 14
10)
Em um triângulo ABC, sabe-se que a=2b e ângulo C=60º.
Calcular os outros 2
ângulos.
Solução:
Aplicando a lei dos cossenos em relação ao vértice C, temos:
c² = a² + b² - 2.a.b.cos60
→ c² = 4b² + b² - 4b².1/2 =
3b² → c = b.√3
Aplicando a lei dos senos, temos:
b/senB = c/sen60 →
b/senB = b√3/(√3/2) → 1/senB = 2 → senB = 1/2
Logo:
senB = 1/2 ↔ x = 30º
Como a soma dos ângulos internos de um triângulo é 180º,
então, temos:
60º + 30º + y = 180º
↔ y = 90º
Solução
11) FUVEST
Em um triangulo ABC o lado AB
mede 4√2 e o ângulo C, oposto ao lado AB, mede 45º. Determine o raio da
circunferência que circunscreve o triângulo.
Solução:
Desenhando o que foi descrito,
temos:
Aplicando a lei dos senos:
Logo:
2.R.sen45º = 4√2
2.R.√2/2 = 4√2 → R = 4
Assim, o raio da circunferência
circunscrita é 4.
12)
Dois lados de um triângulo medem 6m e 10m e formam entre si
um ângulo de 120º. Determinar a medida do terceiro lado.
Vamos fazer o desenho com os dados informados:
Aplicando a Lei dos cossenos:
a² = b² + c² - 2.b.c.cosA
→ x² = 10² + 6² - 2.10.6.cos120º
x² = 100 + 36 -120.(-1/2)
x² = 100 + 36 + 60
x² = 196
x = 14
Portanto, o terceiro lado mede 14 metros .
13) MACK
Calcule
a área do triângulo ABC da figura, sabendo-se que
Solução:
Aplicando no ∆ACD a Lei dos Cossenos, para determinar o ângulo ACD.
(√21)² = 4² + 5² - 2.4.5.cosC
21 = 16 + 25 – 40.cosC
-20 = - 40.cosC
cosC = 1/2 ↔
C = 60º
No ∆ABC, o ângulo
ACB = 180 – 60 = 120º
Logo, o ângulo BAC = 180 – (30 +
120) = 30º
Chegamos à conclusão que o ∆ABC é isósceles, baseado nos ângulos internos. Logo, temos
que AC = BC = 4
Neste momento temos todos os dados
para calcular a área do ∆ABC e usando a fórmula dada.
a = 4
b = 4
α = 120º
A
= (1/2).a.b.senα = (1/2).4.4.sen120º = 8.√3/2
= 4√3 → A = 4√3
Portanto, a área do triângulo (ABC) é igual a 4√3.
14) FUVEST
Calcule
o x da figura.
Solução:
Como
a soma dos ângulos internos de um triângulo é 180º. Portanto, o ângulo ABC é igual a 180 – (75 +
45) = 60º.
Pela
lei dos senos temos que:
x/sen45º = 5/sen60º → x =
5.sen45º/sen60º
x = 5.(√2/2)/(√3/2)
x= 5.√2/√3 ↔
(racionalizando) →
x = (5√6)/3
15) UNIRIO
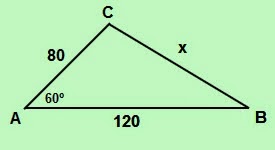
Deseja-se medir a distância entre duas cidades B e C sobre um mapa, sem
escala. Sabe-se que AB = 80km e AC = 120km, onde A é uma cidade conhecida, como
mostra a figura. Determine a distância entre B e C, em km.
Solução:
Vamos aplicar a lei dos cossenos
para calcular o “x”:
x²
= 80² + 120² - 2.80.120.cosA = 6400 + 14400 – 19200.cos60º
x²
= 20800 – 19200.1/2
x²
= 11200
x = √11200 = √112.100 = 10.√112 ≈
10.10,6 = 106
Portanto,
x ≈ 106 km
16) CESGRANRIO
No triângulo ABC, os lados AC e
BC medem 8cm e 6cm, respectivamente, e o ângulo A vale 30º. Quanto vale o seno
do ângulo B?
Solução:
Aplicando a lei dos senos,
temos:
6/sen30º = 8/senB → 6.senB =
8.1/2 → senB = 2/3
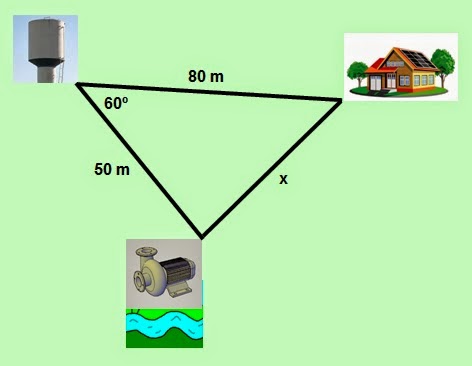
17) UNICAMP
A água utilizada na casa de um
sítio é captada e bombeada do rio para uma caixa-d’água a 50m de distância. A
casa está a 80m de distância da caixa-d’água e o ângulo formado pelas direções
caixa-d’água-bomba e caixa-d’água-casa é de 60º. Se se pretende bombear água do
mesmo ponto de captação até a casa, quantos metros de encanamento são
necessários?
Aplicando
a lei dos cossenos, temos:
x² =
80² + 50² - 2.80.50.cos60º = 8900 – 8000.1/2 = 4900
x² =
4900
x =
√4900 = 70 → x = 70 m
18)
Na
figura abaixo, o triângulo ABC é um triângulo equilátero de 3 cm de lado, e
o triângulo retângulo BCD tem lados BD = 4 cm e CD =
5 cm
e ângulo CBD= 90°.
Solução:
Como
o triângulo ABC é eqüilátero, então o ângulo ABC = 60º.
Logo,
o ângulo ABD é 90 + 60 = 150º.
Pela
lei dos cossenos, temos:
x² =
3² + 4² - 2.3.4.cos150º = 25 – 24.(-√3/2) = 25 + 12.√3
x² =
25 + 12.√3
x = √(25 + 12.√3)
19) UNESP
Dois
terrenos, T1 e T2, têm frentes para a rua R e fundos para a rua S, como mostra
a figura. O lado BC do terreno T1 mede 30 m e é paralelo ao lado DE do terreno T2. A
frente AC do terreno T1 mede 50
m e o fundo BD do terreno T2‚ mede 35 m . Ao lado do terreno T2‚
há um outro terreno, T3, com frente para a rua Z, na forma de um setor circular
de centro E e raio ED.
Determine:
a) as
medidas do fundo AB do terreno T1 e da frente CE do terreno T2.
b) a
medida do lado DE do terreno T2‚ e o perímetro do terreno T3.
Solução:
Fazendo
as seguintes considerações: AB = x e CE
= y.
Aplicando
a lei dos cossenos, temos que:
Pela
lei dos cossenos:
x² =
50² + 30² - 2.50.30.cos120º = 2500 + 900 – 3000.(-1/2) = 4900
x² =
4900
x = 70 m
→ AB = 70 m
Os
triângulos ABC e ADE são semelhantes, portanto:
(50 +
y)/50 = (70 + 35)/70 → (50 + y)/5 = 105/7 →
50 +
y = 5. 15
y =
75 – 50 = 25
y = 25 m → CE = 25 m
Os triângulos ABC e ADE são semelhantes, portanto:
Os ângulos ACB e AED
são iguais e todos os lados são proporcionais:
DE/BC = EA/CA
DE/30 = (25 + 50)/50 = 75/50 = 15/10
DE/30 = 15/10
DE = 45 m
Como o terreno T3 é um setor circular, temos que: ED = EF = 45 = raio.
O ângulo DEF = 180 – 120 = 60
Como 60º corresponde a 1/6 da circunferência inteira (360º),
logo o comprimento do arco é também 1/6 do comprimento total.
Portanto, arco DF = 1/6. 2.π.45 = 15π
Logo, o perímetro do terreno T3 é igual a soma dos lados DF,
ED e EF:
p = 45 + 45 + 15π = 15(6 + π)
p = 15.(6 + π)
20) UFRJ
O
polígono regular representado na figura tem lado de medida igual a 1 cm e o ângulo α mede 120°.
Determine
o raio da circunferência circunscrita.
Solução:
Redesenhando, temos:
Redesenhando, temos:
Vamos
determinar o segmento AB, aplicando a lei dos cossenos:
AB² =
1² + 1² - 2.1.1.cos(120º) = 2 – 2.(-1/2) = 3
AB =
√3 cm
O
raio da circunferência é a metade da diagonal do quadrado de lado √3 cm.
r =
(1/2).d
Por
teorema de Pitágoras:
d² =
(√3)² + (√3)² = 6 →
d = √6 cm
Portanto,
r = √6/2


























Muito bom o trabalho, espero que continue postando mais exercícios. Obrigado..
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluira questão 18 está errada o sinal da resposta
ResponderExcluirObrigado! Corrigido.
ExcluirExercícios muito bons e com solução muito bom mesmo
ResponderExcluirnão entendi a resolução do 2
ResponderExcluirAs respostas estão corretas?
ResponderExcluirtem algumas questões que aparenta está errada.
nossa eu te daria um beijo se te conhecesse, muito obrigaada
ResponderExcluirnice to meet you
Excluir