Demonstração da Lei
dos senos:
Vamos tomar um triângulo ABC qualquer inscrito em uma circunferência de raio r.
A partir do ponto B pode-se encontrar um ponto diametralmente oposto D. Ligando D a C formamos um novo triângulo BCD retângulo em C.
Da figura, podemos perceber também que os ângulos A e D iguais porque enxergam na circunferência a mesma corda BC.
Temos então:
Em triângulo retângulo, seno = cateto oposto/hipotenusa, logo temos que:
Demonstração:
Na figura acima podemos observar que temos 3 triângulos ABC,
BCD e ABD.
Também, temos que: b
= m1 + m2 (1) e
Aplicando o Teorema de Pitágoras nos triângulos BCD e ABD,
temos que:
Como (1) b = m1 + m2 →
m2 = b – m1 e
(4)
c² = h² + m1² →
h² = c² - m1²
Substituindo em (3), temos:
(3) a² = h² + m2² → a² = (c²
- m1²) + (b – m1)²
→ a² = c² - m1² + b²-2bm1 + m1² → a² = b² + c² -2bm1
Como

Então, a² = b² + c² - 2.b.m1
→
Da mesma forma: podemos observar que temos 3 triângulos ABC,
BCF e ACF.
Também, temos que: c = k1 + k2 (5) e
Aplicando o Teorema de Pitágoras triângulos
ABE e ACE, temos que:
Substituindo em (8), temos:
(8) b² = s² + k2² →
b² = (a² - k1²) + (c – k1)² =
a² - k1²
+ c² -2ck1 + k1² → b² = a² + c² - 2ck1 , como
Então,
Da mesma forma: podemos observar que temos 3 triângulos ABC,
ACE e ABE.
Temos que: a = n1 + n2 (9) e
Teorema de Pitágoras nos
triângulos ACE e ABE:
Substituindo em (12), temos:
(12) c² = n2² + t²
→ c² = (a - n1)²
+ b² - n1² =
a² - 2an1
+ n1² + b² - n1² → c² = a² +
b² - 2.a.n1,
como


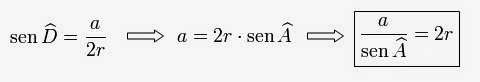















muito bom parabens....
ResponderExcluir