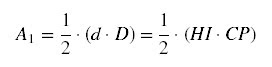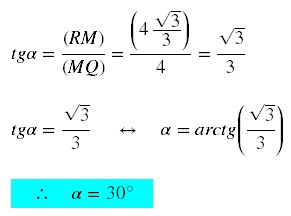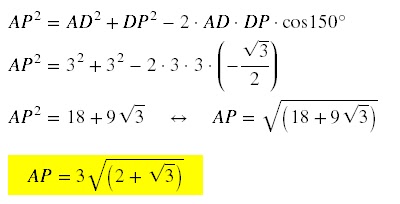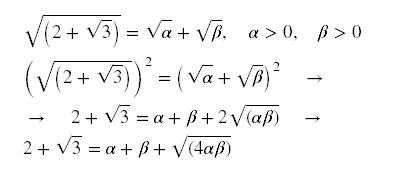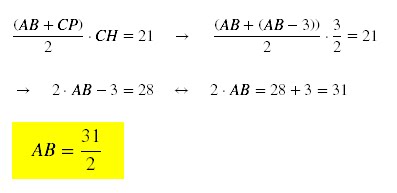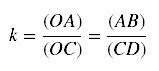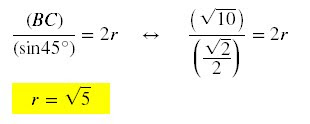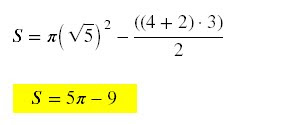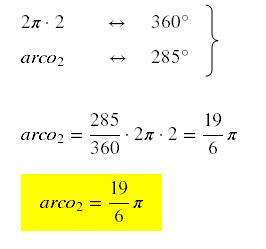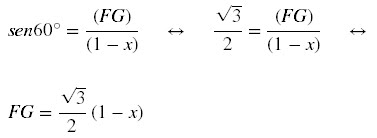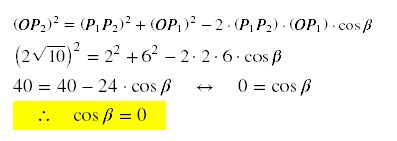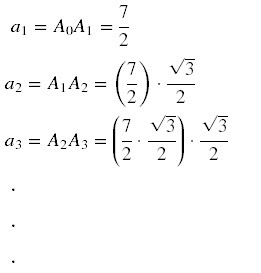Ex-01 (FUVEST 2000)
Considere os pontos
A=(-2,0), B=(2,0), C=(0,3) e P=(0,α), com 0 < α < 3. Pelo ponto P, traçamos as três retas paralelas
aos lados do triângulo ABC.
(a) Determine, em função
de α, a área da região sombreada na figura.
(b) Para que valor de α
essa área é máxima?
Solução:
a)
Redesenhando convenientemente, temos:
Observando a figura, temos:
1) O triângulo ABC é
isósceles.
2) O quadrilátero CHPI é
um losango cujo diagonal menor HI (=d) e diagonal maior CP (=D). Portanto, a
área é calculada da seguinte forma:
Ainda podemos observar que
os segmentos FP e HI são iguais (FP=HI).
3) Os quadriláteros PEAG e
PFBD são iguais e paralelogramos cujas bases são EA e DB respectivamente e
altura de ambos são PO.
4) Os triângulos ∆BMC
e ∆DMP são semelhantes, então podemos calcular a base
do paralelogramo de seguinte maneira:
5) Os triângulos ∆BMC
e ∆FPC são semelhantes, então podemos calcular a
diagonal menor do losango de seguinte maneira:
Da figura temos que (FP) = (HI).
Redesenhando, temos:
A
área A correspondente à parte
sombreada é igual a:
b)
O valor de α
para área máxima é a abscissa do vértice.
Como o coeficiente de α²
é negativo, a parábola tem a concavidade virada para baixo:
O valor de alfa do vértice pode ser obtido igualando a
primeira derivada da expressão de área à zero.
Ex-02 (FUVEST 2000)
No quadrilátero ABCD da figura a seguir, E é um ponto sobre o lado AD tal que o ângulo ABE mede 60º e os ângulos EBC e BCD são retos. Sabe-se ainda que AB = CD = √3 e BC = 1. Determine a medida de AD.
Solução:
Vamos calcular o valor do
ângulo θ (=ângulo DBC).
Como o ângulo θ =
60º, então o ângulo EBD = 90º - 60º = 30º, portanto o triângulo ABD é também
retângulo.
Logo, aplicando o Teorema
de Pitágoras, temos:
Resposta: A medida de AD = √7
Ex-03 (FUVEST 2001)
Onde A e B são os pontos
médios das alturas do retângulo. Sabendo-se ainda que os pontos A, B e O estão
alinhados e que BO =20 m, determine
(a) a área da intersecção
das regiões irrigadas pelas máquinas;
(b) a área total irrigada.
Utilize as seguintes
aproximações: √2 = 1,41; π = 3,14 e arcsen(1/3) = 0,340
rad.
Solução:
Para calcular a
intersecção das regiões irrigadas, pela figura, temos:
Área do quadrilátero CDEF
somado ao resultado da área do setor circular COD subtraído pela área do
triângulo COD.
Sejam
S1 = área do setor circular COD;
S2 = área do triângulo COD;
S3 = área do quadrilátero CDEF;
SI = área correspondente à intersecção das regiões irrigadas.
ST = área total irrigada
a) A área da intersecção das regiões irrigadas é dada por:
Ex-04 (FUVEST 2002)
(a) o comprimento dos segmentos CN e CM;
Solução:
Assim,
Ex-05 (FUVEST 2002)
Na figura abaixo, as circunferências C1 e C2, de centros O1 e O2, respectivamente, se interceptam nos pontos P e Q. A reta r é tangente a C1 e C2; a reta s passa por O1 e O2 e β é o ângulo agudo entre r e s. Sabendo que o raio de C1 é 4, o de C2 é 3 e que o senβ=1/5, calcule:
(a) a área do quadrilátero O1QO2P;
(b) senα, onde α=QO2P.
Solução:
Desenhando conforme as informações dadas, temos:
(b) senα, onde α=QO2P.
Solução:
Desenhando conforme as informações dadas, temos:
Como O1O2 = 5, O1P = 4 e O2P = 3, temos que (O1O2)² = (O1P)² + (O2P)² que é uma condição para um terno pitagórico. Logo ∆PO1O2 é um triângulo retângulo em P.
Portanto,
a)
A área do quadrilátero O1QO2P é:
No triângulo ∆PO1O2, tem-se:
Então:
Ex-06 (FUVEST 2003)
(a) O raio da circunferência.
(b) A medida do ângulo POQ, onde O é o centro da circunferência.
Solução:
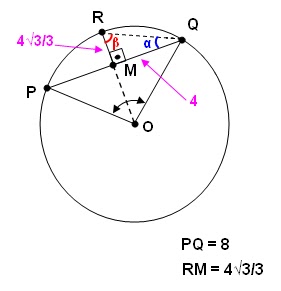
O triângulo ∆MQR é retângulo em M, então, podemos escrever que:
(b) A medida do ângulo POQ, onde O é o centro da circunferência.
Solução:
O triângulo ∆ROQ é isósceles, então, os ângulos ORQ e RQO possuem valores iguais. Assim, tem-se: ORQ = RQO = α = 60º.
Logo, no triângulo ∆ROQ temos que: ORQ + RQO + ROQ = 180º, então, ROQ = 60º. Logo o triângulo ∆ROQ é eqüilátero. Portanto, os lados OR = OQ = RQ.
a)
Aplicando Pitágoras no ∆MQR:
(a) cosABQ
(b) cosABP
(c) cosQBP
Solução:
a)
De enunciado:
O triângulo ∆ABQ
é retangular em Q, então:
b)
Aplicando a lei dos
cossenos ao triângulo ∆ABP, tem-se:
c)
Ex-08 (FUVEST 2003)
Solução:
Seja o ponto P médio de
BC, então, tem-se:
Ex-09 (FUVEST 2004)
Solução:
Ex-10 (FUVEST 2004)
Assim, o arco P2Q2 tem a medida angular igual a:
Ex-11 (FUVEST 2004)
(a) o valor de r;
(b) a área da região hachurada.
Solução:
Podemos expressar a medida do segmento O1O3 de seguintes formas:
A área da região hachurada é igual à:
Área do quadrado O1O2O3O4, subtraído a área do círculo de raio 2 e área correspondente à 4 setores circulares de raio r e ângulo de 90º:
Ex-12 (FUVEST 2005)
Na figura acima, as 12 circunferências têm todas o mesmo raio r; cada uma é tangente a duas outras e ao quadrado. Sabendo-se que cada uma das retas suporte das diagonais do quadrado tangencia quatro das circunferências (ver figura) e que o quadrado tem lado 2√7, determinar r.
Solução:
Completando o desenho com as informações dadas e fazendo uma revisão conveniente para resolver o problema, temos:
Solução:
Completando o desenho com as informações dadas e fazendo uma revisão conveniente para resolver o problema, temos:
Calculando o x:
Ex-13 (FUVEST 2006)
Na figura abaixo, O é o
centro da circunferência de raio 1,
a reta AB é secante a ela, o ângulo β mede 60º e senα = √3/4.
(a) Determine senOÂB em
função de AB.
(b) Calcule AB.
Solução:
Se AB é secante, então o
∆BCO é isósceles e como β = 60º, então, o triângulo ∆BCO é eqüilátero.
a)
Pela lei dos senos, temos:
b)
Logo,
temos que:
Ex-14 (FUVEST 2006)
No paralelogramo ABCD abaixo, tem-se que AD = 3 e
DÂB = 30º. Além disso, sabe-se que o ponto P pertence ao lado DC e à bissetriz
do ângulo DÂB.
(a) Calcule AP.
(b) Determine AB sabendo
que a área do quadrilátero ABCP é 21.
Solução:
Sabemos que:
Paralelogramos são figuras geométricas que possuem apenas quatro lados,
sendo os lados opostos paralelos e medidas iguais. Como todo quadrilátero, a
soma dos ângulos internos é de 360º. Possui duas diagonais que se cruzam no
ponto médio e os ângulos opostos possuem medidas iguais.
a)
Pela Lei dos Cossenos,
temos:
Neste caso, podemos obter
a mesma resposta, porém, de outra aparência; vamos fazer algumas manipulações
algébricas:
Por comparação, temos:
Assim, temos:
b)
A área do quadrilátero
ABCP (que é trapézio) é igual
No triângulo BCH, tem-se:
Então, temos:
Ex-15 (FUVEST 2007)
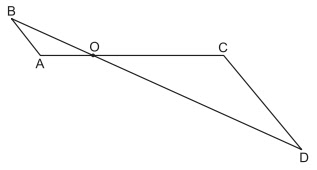
Na figura abaixo, os segmentos AB e CD são
paralelos, o ângulo OAB mede 120º, AO = 3 e AB = 2. Sabendo-se ainda que a área
do triângulo OCD vale 600√3.
(a) calcule a área do
triângulo OAB.
(b) determine OC e CD.
Solução:
a)
A área do ∆OAB é:

b)
Considerando que o ponto O
seja a intersecção dos segmentos AC e BD e como AB e CD são paralelos, então,
os triângulos OAB e OCD são semelhantes.
A razão de semelhança é:
Assim, temos:
Ex-16 (FUVEST 2007)
A figura representa um
trapézio ABCD de base AB e CD, inscrito em uma circunferência cujo centro O
está no interior do trapézio. Sabe-se que AB = 4, CD = 2 e AC = 3√2.
(a) Determine a altura do
trapézio.
(b) Calcule o raio da
circunferência na qual está inscrito.
(c) Calcule a área da
região exterior ao trapézio e delimitada pela circunferência.
Solução:
a)
O trapézio ABCD é
isósceles, pois, m(C) = m(D), m(A) = m(B) e AB é paralelo a CD.
Então, temos:
Pitágoras no ∆ACH, temos:
b)
Considerando r o raio do círculo, então temos:
Pela lei dos senos:
c)
A área da região
solicitada é a diferença entre a área do circulo de raio r = √5 e a área do
trapézio ABCD, então,
Ex-17 (FUVEST 2008)
No triângulo ABC, tem-se
que AB > AC, AC = 4 e cosC = 3/8. Sabendo-se que o ponto R pertence ao
segmento BC e é tal que AR = AC e BR/BC = 4/7, calcule
(a) a altura do triângulo
ABC relativa ao lado BC.
(b) a área do triângulo
ABR.
Solução:
a)
Por Pitágoras no ∆ACH,
tem-se:
b)
Ex-18 (FUVEST 2008)
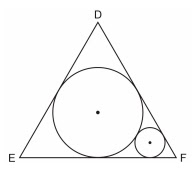
O círculo C, de raio R,
está inscrito no triângulo eqüilátero DEF. Um círculo de raio r está no
interior do triângulo DEF e é tangente externamente a C e a dois lados do
triângulo, conforme a figura.
Assim, determine
(a) a razão entre R e r.
(b) a área do triângulo
DEF em função de r.
Solução:
a)
Os triângulos AFO e BFP
são retângulos e semelhantes, então, temos:
b)
Por Pitágoras no triângulo
∆DFM; tem-se:
Ex-19 (FUVEST 2009)
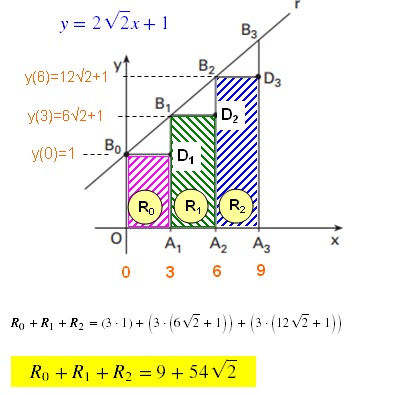
Na figura ao lado, a reta
r tem equação y = 2√2x + 1 no plano cartesiano Oxy. Além disso, os pontos B0,
B1, B2, B3 estão na reta r, sendo B0
= (0,1). Os pontos A0, A1, A2, A3
estão no eixo Ox, com A0 = O = (0,0). O ponto Di, pertence ao segmento AiBi,
para 1 ≤ i ≤ 3. Os segmentos A1B1, A2B2,
A3B3 são paralelos ao eixo Ou, os segmentos B0D1,
B1D2, B2D3 são paralelos ao eixo
Ox, e a distância entre Bi e Bi+1 é igual a 9, para 0 ≤ i
≤ 2.
Nessas condições:
(a) Determine as abscissas
de A1, A2, A3.
(b) Sendo Ri, o
retângulo de base AiAi+1 e altura Ai+1Di+1,
para 0 ≤ i ≤ 2, calcule a soma das áreas dos retângulos R0, R1
e R2.
O coeficiente angular da reta r:
Por Pitágoras:
Portanto, as abscissas de
A1, A2 e A3 são:
b)
Ex-20 (FUVEST 2009)
Na figura, estão
representadas a circunferência C, de centro O e raio 2, e os pontos A, B, P e
Q, de tal modo que:
(1) O ponto O pertence ao
segmento PQ.
(2) OP = 1, OQ = √2.
(3) A e B são pontos da
circunferência, AP ┴ PQ e BQ ┴ PQ.
Assim sendo, determine:
(a) A área do triângulo
APO.
(b) Os comprimentos dos
arcos determinados por A e B em C.
(c) A área da região
hachurada.
Solução:
a)
Por Teorema de Pitágoras, tem-se:
Assim,
b)
No triângulo ∆AOP:
No triângulo ∆BOQ:
Então temos que:
Calculando o comprimento
dos arcos:

c)
A área da parte hachurada
é:
Ex-21 (FUVEST 2009)
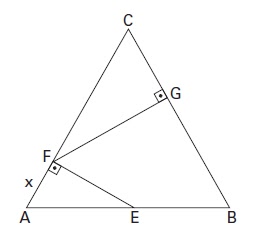
O triângulo ABC da figura ao lado é equilátero
de lado 1. Os pontos E, F e G pertencem, respectivamente, aos lados AB, AC e BC
do triângulo. Além disso, os ângulos AFE e CGF são retos e a medida do segmento
AF é x. Assim, determine:
(a) A área do triângulo
AFE em função de x.
(b) O valor de x para o
qual o ângulo FÊG também é reto.
Solução:
a)
A área do triângulo
retângulo AEF é:
b)
No triângulo retângulo
CFG, temos:
No triângulo retângulo
EFG, temos:
Ex-22 (FUVEST 2010)
No triângulo ABC da
figura, a mediana AM, relativa ao lado BC, é perpendicular ao lado AB. Sabe-se
também que BC = 4 e AM = 1. Se α é a medida do ângulo ABC, determine:
(a) senα;
(b) o comprimento AC;
(c) a altura do triângulo
ABC relativa ao lado AB;
(d) a área do triângulo
AMC.
Solução:
a)
b)
Os triângulos ∆ABM e ∆BCH
são semelhantes, portanto, temos:
Também, podemos escrever
que:
Por comparação, temos:
Por semelhança de
triângulos temos:
Por Pitágoras, temos:
c)
Do item anterior (b),
temos:
d)
Se senα = 1/2, então, α =
30º, logo θ = 60º. Então, β = 120º.
Portanto, temos:
Ex-23 (FUVEST 2011)
As circunferências C1
e C2 estão centradas em O1 e O2, têm raios r1
= 3 e r2 = 12, respectivamente, e tangenciam-se externamente. Uma
reta t é tangente a C1 no ponto P1, tangente a C2
no ponto P2 e intercepta a reta O1O2 no ponto
Q. Sendo assim, determine
(a) o comprimento P1P2;
(b) a área do quadrilátero
O1O2P2P1;
(c) a área do triângulo QO2P2.
Solução:
a)
Por Pitágoras no triângulo ∆AO1O2,
temos:
b)
O quadrilátero O1O2P2P1
é um trapézio, então, temos:
c)
Os triângulos ∆QO2P2
e ∆O1O2A são semelhantes, então, temos:
Ex-24 (FUVEST 2012)
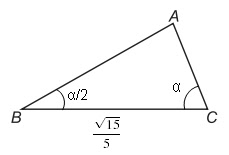
No triângulo acutângulo
ABC, ilustrado na figura, o comprimento do lado BC mede √15/5, o ângulo interno
de vértice C mede α, e o ângulo interno de vértice B mede α/2. Sabe-se, também,
que 2cos(2α)+3cosα+1=0.
Nessas condições, calcule
a) o valor de senα
b) o comprimento do lado
AC.
Solução:
a)
Sabemos que: cos(2α) =
2cos²α ‒ 1 e seja 2cos(2α)+3cosα+1=0, temos:
b)
A figura com os dados do
enunciado:
Traçando a bissetriz do
ângulo BCA, temos:
1 - O triângulo ∆BCD é
isósceles.
2 - Os triângulos ∆ABC e
∆ACD são semelhantes.
∆BCD
Aplicando lei dos
cossenos, temos:
∆ABC e ∆ACD
Assim, podemos escrever
que:
Ex-25 (FUVEST 2012)
Na figura, a
circunferência de centro O é tangente à reta CD no ponto D, o qual pertence à
reta AO. Além disso, A e B são pontos da circunferência, AB = 6√3 e BC = 2√3.
Nestas condições, determine
a) a medida do segmento
CD;
b) o raio da
circunferência;
c) a área do triângulo
AOB;
d) a área da região
hachurada na figura.
Solução:
a) Aplicando o Teorema da
Secante-Tangente, temos:
b) O triângulo ACD é
retângulo em D, portanto, pela aplicação do Teorema de Pitágoras, temos:
c) Seja BH a altura do
triângulo ∆AOB em relação ao lado AO. Assim, os triângulos ∆ABH e ∆ACD são
semelhantes, então temos:
Portanto, a área do ∆AOB
é:
d)
Assim, β =
120º, então,
Ex-26 (FUVEST 2013)
Percorre-se o
paralelogramo ABCD em sentido anti-horário. A partir de cada vértice atingido
ao longo do percurso, prolonga-se o lado recém- percorrido, construindo-se um
segmento de mesmo comprimento que esse lado.
As extremidades dos prolongamentos são denotadas por A’, B’, C’ e D’, de
modo que os novos segmentos sejam, então, AA’, BB’, CC’ e DD’. Dado que AB = 4 e que a distância de D à reta
determinada por A e B é 3, calcule a área do
a) paralelogramo ABCD;
b) triângulo BB’C’;
c) quadrilátero A’B’C’D’.
Solução:
a)
A distância do ponto D ao
lado AB fornecida é a altura do paralelogramo, então:

b)
Como conhecemos a área do
paralelogramo ABCD, se desenhar paralelogramos côngruos ao seu redor podemos
calcular facilmente as áreas solicitadas nos itens b e c.
A área do ∆BB’C’ é a
metade da área do quadrilátero BB’PC’, sendo esta é igual ao dobro da área do
paralelogramo ABCD, logo:
Ex-27 (FUVEST 2013)
Um guindaste, instalado em um terreno plano, tem
dois braços articulados que se movem em um plano vertical, perpendicular ao
plano do chão.
Na figura, os pontos O, P1
e P2 representam, respectivamente, a articulação de um dos braços
com a base, a articulação dos dois braços e a extremidade livre do
guindaste. O braço OP1 tem
comprimento 6 e o braço P1P2 tem comprimento 2. Num dado
momento, a altura de P2 é 2, P2 está a uma altura menor
do que P1 e a distância de O a P2 é 2√10. Sendo Q o pé da
perpendicular de P2 ao plano do chão, determine
a) o seno e o cosseno do
ângulo P2OQ entre a reta OP2 e o plano do chão;
b) a medida do ângulo OP1P2
entre os braços do guindaste;
c) o seno do ângulo P1OQ
entre o braço OP1 e o plano do chão.
Solução:
a)
Pela figura temos que:
Pela relação fundamental
de trigonometria, temos o valor do cosseno de α:
b)
Pela Lei dos Cossenos no
∆OP1P2, temos:
c)
Como β=90º, então os
triângulos ∆OP1P2 e ∆OP2Q são congruentes,
logo OQ = 6.
Ou pela aplicação de
Pitágoras no ∆OP2Q, temos:
Ex-28 (FUVEST 2014)
Uma bola branca está
posicionada no ponto Q de uma mesa de bilhar retangular, e uma bola vermelha,
no ponto P, conforme a figura ao lado. A reta determinada por P e Q intersecta
o lado L da mesa no ponto R. Além disso, Q é o ponto médio do segmento PR, e o
ângulo agudo formado por PR e L mede 60º. A bola branca atinge a vermelha, após
ser refletida pelo lado L. Sua
trajetória, ao partir de Q, forma um ângulo agudo θ com o segmento PR e o mesmo
ângulo agudo α com lado L antes e depois da reflexão. Determine a tangente de α
e o seno de θ.
Solução:
Pela figura, temos que:
1) O triângulo ∆PRP’ é
isósceles.
2) O pontos Q e Q’ são
pontos médios de PR e RP’ respectivamente, então o ponto S é o baricentro do
triângulo ∆PRP’, logo RS = 2SM (1).
3) No triângulo ∆RPM,
Calculando a tangente de α
no triângulo ∆PSM:
Aplicando a Lei dos Senos
no triângulo ∆RSQ, temos:
De triângulo ∆PSM:
Para determinar o valor
PS, pelo teorema de Pitágoras, temos:
Ex-29 (FUVEST 2014)
Considere o triângulo
eqüilátero ∆A0OB0 de lado 7 cm .
a) Sendo A1 o
ponto médio do segmento A0B0 e B1 o ponto
simétrico de A1 em relação à reta determinada por O e B0,
determine o comprimento de OB1.
b) Repetindo a construção
do item (a), tomando agora como ponto de partida o triângulo ∆A1OB1,
pode-se obter o triângulo ∆A2OB2 tal que A2 é
o ponto médio do segmento do segmento A1B1, e B2
o ponto simétrico de A2 em relação à reta determinada por O e B1.
Repetindo mais uma vez o procedimento, obtém-se o triângulo ∆A3B3.
Assim, sucessivamente, pode-se construir uma sequência de triângulo ∆AnOBn tais
que, para todo n≥1, An é o ponto médio de An-1Bn-1, e Bn, o ponto simétrico de An
em relação à reta determinada por O e Bn-1, conforme a figura. Denotando por an,
para n≥1, o comprimento do segmento An-1An, verifique que a1, a2, a3, ... é uma
progressão geométrica. Determine sua razão.
c) Determine, em função de
n, uma expressão para o comprimento da linha poligonal A0A1A1....An,
n ≥ 1.
O ponto P’ é simétrico ao
ponto P em relação à reta r se o segmento PP’ é perpendicular à reta r e a
intersecção de PP’ e r é o ponto médio de PP’.
Solução:
a)
O comprimento do segmento
OB1 é igual à altura do triângulo eqüilátero A0OB0.
Portanto,
b)
Seja q a razão do PG
(progressão geométrica), então:
c)
O comprimento da linha
poligonal é a soma dos n primeiros termos da PG definido no item anterior.
Portanto, temos:
Ex-30 (FUVEST 2016)
São dadas três
circunferências de raio r, duas a duas tangentes. Os pontos de tangências são P1,
P2 e P3.
Calcule, em função de r.
a) o comprimento do lado
do triângulo eqüilátero T determinado pelas três retas que são definidas pela
seguinte exigência: cada uma delas é tangente a duas das circunferências e não
intersecta a terceira.
b) a área do hexágono não
convexo cujos lados são os segmentos ligando cada ponto P1, P2
e P3 aos dois vértices do triângulo T mais próximos a ele.
Solução:
a)
Pela figura temos:
b)
Seja S representação de
área, então, pela figura, temos:
Logo, a área do hexágono
não convexo AP1BP2CP3 é: